Blog

Introduction

Pythagorean triplets, a fascinating concept in mathematics, involve three numbers where the square of one number added to the square of another equals the square of the third. When given an array of numbers, the quest is to uncover whether such a unique triplet exists within it.

Question

Given an array of n integers, the task is to create a function that determines whether there exists a Pythagorean triplet (a, b, c) within the array such that a2+b2=c2. Return true if a Pythagorean triplet exists; otherwise, return false.

Example:

• Input: N=5, Array = {3, 2, 4, 6, 5}
  • Output: Yes
  • Explanation: For the given array, a=3, b=4, and c=5 form a Pythagorean triplet.
• Input: N=3, Array = {3, 8, 5}
  • Output: No
  • Explanation: There’s no Pythagorean triplet possible for this array.

Your Task: Implement the function checkTriplet() which receives an array arr and a single integer n as input. The function should return true if a Pythagorean triplet exists in the array; otherwise, it should return false. The driver code will print “Yes” or “No” based on the boolean value returned.

Constraints:
1 <= n <= 10⁵
1 <= arr[i] <= 1000

How To Approach

1. Understand the Goal: We aim to discover if there exist three numbers (a, b, c) within the given array such that when you square ‘a’ and ‘b’ and then add them together, the result matches the square of ‘c’.
2. Iterate Through the Array: Start by going through the array elements. For each number ‘a’, look for another number ‘b’ by running a loop starting from ‘a+1’ to the end of the array.
3. Check for Triplet Conditions: Calculate the sum of squares of ‘a’ and ‘b’ and search if this sum exists as a square in the array.
4. Return Result: If such a match is found, return true as there exists a Pythagorean triplet; otherwise, return false.
5. Explanation: Once the code is executed, it checks each number in the array. It computes the sum of squares of pairs and searches for a matching square within the array. If a match is found, it confirms the existence of a Pythagorean triplet.

Solution Code (C++)

Below code you have to run in Geeks of Geeks Coding place:-

class Solution {
public:
    // Function to check if the Pythagorean triplet exists or not
    bool checkTriplet(int arr[], int n) {
        unordered_set<int> squaredSet;

        // Create a set to store the squares of elements in arr
        for (int i = 0; i < n; i++) {
            squaredSet.insert(arr[i] * arr[i]);
        }

        // Check for the Pythagorean triplet
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int sumOfSquares = arr[i] * arr[i] + arr[j] * arr[j];
                // Check if the sum of squares is present in the squaredSet
                if (squaredSet.find(sumOfSquares) != squaredSet.end()) {
                    return true;
                }
            }
        }
        return false;
    }
};

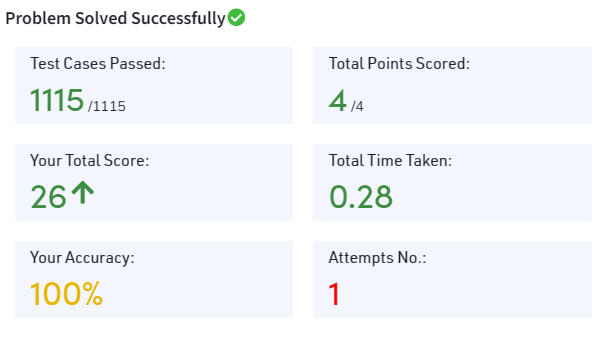
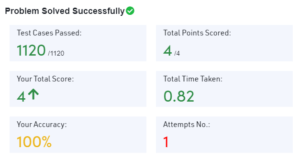
Explanation:

1. Creating a Set for Squares:
   • The function begins by creating an unordered_set named squaredSet to store the squares of the elements in the array.
   • It iterates through the array and inserts the square of each element into this set.
2. Checking for Pythagorean Triplets:
   • The function then runs two nested loops to examine each pair of elements in the array.
   • For each pair (a, b), it computes the sum of squares of the two numbers.
   • Subsequently, it checks if this sum of squares is present in the squaredSet.
   • If it finds a match, it immediately returns true, signifying the presence of a Pythagorean triplet.
3. Handling No Triplet Found:
   • In case the loops complete without finding a match in the squaredSet for any pair’s sum of squares, the function returns false, indicating the absence of a Pythagorean triplet in the array.

Conclusion

The provided function presents a concise and efficient solution to detect Pythagorean triplets within an array. By leveraging a set to store the squares of array elements and checking for matching pairs, it accurately identifies whether a Pythagorean triplet exists.

Visit SixMedium to explore more straightforward solutions to intriguing coding challenges and enhance your knowledge!