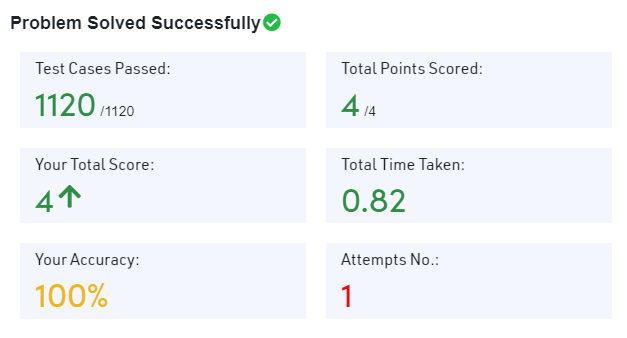
Have you ever wondered how to efficiently calculate the number of ways you can make a certain sum using different coin denominations? In this blog post, we’ll explore a classic coding problem known as the “Coin Change Problem” and demonstrate how to solve it using dynamic programming in Java 1.8.

The Coin Change Problem:

Given an array coins representing different denominations of currency, and an integer sum, your task is to find the number of ways you can make the sum by using different combinations of the coins. You can assume that you have an infinite supply of each type of coin, and you can use any coin as many times as you want.

For example:

Example 1:

Input:
N = 3, sum = 4
coins = {1, 2, 3}
Output: 4
Explanation: Four possible ways are: {1, 1, 1, 1}, {1, 1, 2}, {2, 2}, and {1, 3}.

Example 2:

Input:
N = 4, Sum = 10
coins = {2, 5, 3, 6}
Output: 5
Explanation: Five possible ways are: {2, 2, 2, 2, 2}, {2, 2, 3, 3}, {2, 2, 6}, {2, 3, 5}, and {5, 5}.

Your task is to implement the count method inside the Solution class. The method should accept an array of coin denominations coins, its size N, and the target sum sum. It should return the number of ways to make the given sum using the provided coins.

Java Implementation:

class Solution {
    public long count(int coins[], int N, int sum) {
        // Your dynamic programming code here
    }
}

In the next section, we’ll walk through the dynamic programming solution to the Coin Change Problem using the provided Java code. So, let’s jump into the details and understand how to tackle this problem step by step!

Let’s approach this problem:

Step 1: Understand the Problem

We’re given a set of coin denominations and a target sum. The goal is to find the number of ways we can use these coins to make up the given sum. We can use each coin as many times as we want.

Step 2: Dynamic Programming Approach

To solve this problem efficiently, we’ll use a technique called dynamic programming. Dynamic programming helps us break down a complex problem into simpler subproblems and build solutions from those subproblems.

Step 3: Initialize the DP Array

We’ll create an array called dp, where each element dp[i] will represent the number of ways to make the sum i using the given coins. We’ll start by setting dp[0] to 1, because there’s exactly one way to make the sum 0, which is by not using any coins.

Step 4: Iterating Through Coins

For each coin denomination, we’ll loop through the dp array starting from that coin’s value. For example, if the coin is worth 2, we’ll start from dp[2]. This is because we want to find the number of ways to make each sum using the current coin and the previously calculated solutions.

Step 5: Update DP Values

While looping through the dp array, we’ll update the values. For each sum i, we’ll add the number of ways we can make the sum i - coin (the remaining amount after using the current coin). This step accounts for the fact that we can use the same coin multiple times.

Step 6: Final Result

After iterating through all the coins, we’ll have the dp array updated with the number of ways to make each sum using the given coins. The final answer will be stored in dp[sum], which represents the number of ways to make the target sum.

Step 7: Implement the Java Code

We’ll implement the above steps in the count method inside the Solution class. This method takes the array of coin denominations, its size, and the target sum as inputs. It returns the final answer.

By using this dynamic programming approach, we efficiently calculate the number of ways to make the desired sum using different coin denominations. This method helps us avoid redundant calculations and solve the Coin Change Problem in an optimized manner.

ANSWER: JAVA

class Solution {
    public long count(int coins[], int N, int sum) {
        // Create a DP array to store the number of ways for each sum
        long dp[] = new long[sum + 1];
        
        // Base case: There's only one way to make sum 0, which is by not using any coins
        dp[0] = 1;

        // Loop through each coin denomination
        for (int coin : coins) {
            // Update the DP array for each sum from coin value to target sum
            for (int i = coin; i <= sum; i++) {
                // Add the ways to make (i - coin) to the current sum's ways
                dp[i] += dp[i - coin];
            }
        }

        // The final answer is stored in dp[sum]
        return dp[sum];
    }
}

Conclusion:

In this guide, we’ve demystified the Coin Change Problem using the power of dynamic programming. By strategically breaking down the problem into smaller parts and efficiently calculating coin combinations, we’ve harnessed a versatile problem-solving technique. Armed with the provided Java code, you’re now equipped to confidently solve the Coin Change Problem and similar challenges. As you embark on your coding journey, remember that dynamic programming offers a structured approach to unravel even the most intricate problems. Happy coding and may your coding endeavors be both rewarding and enlightening!